LE TRAITEMENT MATHÉMATIQUE THÉORIQUE
DE LA QUESTION
52

TRACE THEORIQUE DE LA SURFACE D'UNE MASSE DE GLACE EN ECOULEMENT

On sait que, en régime établi, que l'altitude de la surface d'une masse de glace de largeur infinie, libre de se mouvoir sur une pente, est donnée par la formule de Nye - Lliboutry [L. Lliboutry, 1975], démontrée à partir des propriétés physiques de la glace ( nous l'appellerons dans tout ce qui suit : la formule ) :


où : h = altitude de la glace (en mètres) en un point situé à une distance d (en mètres) du front de la masse de glace,
h° = altitude de ce front.
Cette formule est valable également pour les glaciers de vallée "en première approximation" [Monjuvent, 1978].

Est-il possible de préciser cette affirmation ?
C'est ce que nous nous proposons de faire dans cette page.

Nous signalerons au lecteur pressé qu'il pourra passer directement à la CONCLUSION qui figure en bas de page.
Nous ne saurions cependant trop lui conseiller de parcourir, ne fût-ce que rapidement, la totalité de celle-ci.


Les résultats obtenus pour les différentes vallées étudiées, que l'on pourra examiner dans les pages correspondantes, montrent fréquemment un bon accord entre la formule et la position des sites caractéristiques dans les parties moyennes et basses des vallées alpines.
On consultera en particulier le graphique relatif à la vallée de la Durance, qui figure ci-dessous.

Certains pourront toutefois s'étonner que la surface d'un glacier puisse être ramenée à une formule mathématique, simple de surcroît et dans laquelle le modelé du terrain sous-jacent n'intervient pas. L'examen des glaciers actuels peut effectivement en faire douter.
Mais n'oublions pas que les glaciers que nous avons actuellement sous les yeux diffèrent des grands appareils quaternaires par leur taille, beaucoup plus modeste (à l'exception toutefois des grandes calottes telles que celles du Groenland et de l'Antarctique).
Si les formes des glaciers actuels sont sensiblement les mêmes que celles des grands appareils quaternaires, ainsi que nous l'avons vu à la page différents types de glaciers, de nombreuses différences apparaissent lorsqu'on les examine dans le détail.
Qui, à l'examen d'un paysage au crépuscule, pourrait avoir idée de la splendeur du plein soleil ?
Au risque de choquer certains Disons qu'il existe la même différence entre les gigantesques fleuves de glace du Quaternaire et nos glaciers maigrichons actuels qu'entre une belle pomme, pleine, luisante ..... et le trognon qui marque sa fin.
Les appareils actuels, avec leurs faibles dimensions, sont sensibles aux irrégularités du fond des vallées et aux variations de leur largeur, qu'ils traduisent par des ruptures de pente et des chutes de séracs.
Jean Giono dirait que sous leur peau, on devine les os de la montagne.
Les grands glaciers quaternaires des Alpes présentaient, quant à eux, des épaisseurs qui pouvaient atteindre 1000 m, voire même 2000 m au-dessus des ombilics et leur largeur atteignait parfois 30 km.
C'est ainsi que du col des Aravis jusqu'aux contreforts du Mont Blanc s'étendait une "Mer de Glace" large de 25 km.
La surface des glaciers pouvait donc suivre d'assez près la formule théorique qui traduit l'indifférence quasiment parfaite des grands appareils quaternaires aux irrégularités de leurs lits.



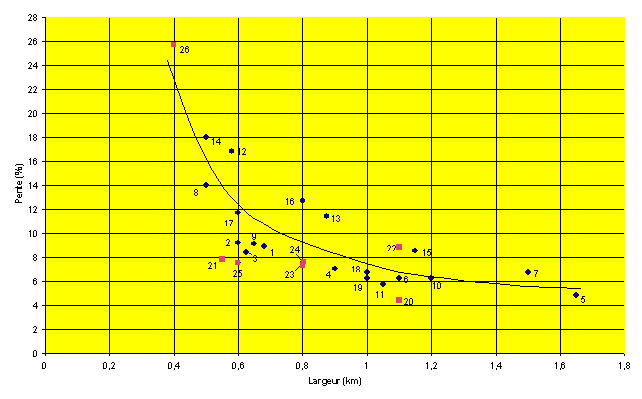
LE DOMAINE DE VALIDITE DE LA FORMULE DE NYE-LLIBOUTRY
Comme la plupart des formules, celle-ci possède un domaine de validité dont il convient, avant toute chose, de bien préciser les limites.
Reprenons donc les termes de l'énoncé qui précède.

1 - ..... « en régime établi » ..... , c'est-à-dire qu'elle ne s'applique pas lors d'une variation rapide du débit du glacier, encore moins, bien entendu, dans le cas d'un surge (pour en savoir plus sur les surges, cliquer ici).
2 - ..... « une masse de glace de largeur infinie ». Ceci permet d'effectuer les calculs dans un plan de figure.
On est donc en droit de considérer que la formule s'applique également à une masse de glace comprise entre deux parois, à condition que celles-ci soient parallèles et assez éloignées pour ne pas apporter d'effet perturbateur dû aux frottements.
Les lignes de courant sont alors parallèles.
Dans le cas d'une vallée étroite interviendrait ce que nous avons appelé un « effet de paroi ».

3 - Mais la masse de glace peut n'être pas limitée par des parois parallèles, l'une des deux - voire les deux - pouvant faire défaut. C'est le cas par exemple pour un glacier de calotte ou lorsque, parvenu dans les plaines de piémont, un glacier de vallée s'étale en lobe.
Les lignes de courant sont alors divergentes.
Intervient alors ce que nous avons appelé un « effet de lobe ».

4 - La formule complète est plus complexe que celle qui figure ci-dessus, des termes du second ordre apparaissant lorsqu'on se situe très près du front de la masse de glace.
La formule ne s'applique donc pas dans les dernières longueurs du glacier, où intervient alors un « effet de langue ».

5 - ..... « libre de se mouvoir sur une pente » ..... .
C'est le cas général des glaciers de vallée, mais il existe des exceptions, par exemple lorsqu'un glacier, diffluant par un col, rejoint un appareil plus important qui lui fixe son niveau aval (voir le glacier rissien de la Durance).

6 - C'est également le cas des glaciers se terminant dans l'océan, où intervient alors ce que nous avons appelé un « effet de flottaison ».

Il convient donc de tenir compte de ces divers « effets », que nous allons maintenant détailler.




L'EFFET DE PAROI

Le premier effet, le plus répandu - et qui nous intéressera au premier chef dans le cadre de cette étude - se rencontre essentiellement dans les parties hautes des vallées.

Considérons par exemple la Romanche. Au-dessus du Bourg d'Oisans (Isère), la formule indique une altitude de la surface du glacier würmien égale à 1500 m, alors que des dépôts morainiques de cette époque peuvent être observés jusqu'à 1760 m au-dessus du Bourg, sur l'arête joignant le col du Solude (photo ici) à Prégentil.
Ces dépôts renferment de nombreux éléments cristallins, alors que le bassin versant de Villard-Reymond n'est formé que de terrains sédimentaires ; ils n'ont donc pu être déposés ici que par le glacier de la Romanche [ carte géologique au 1/50 000 Vizille ].

Cette constatation est générale : dans le haut des vallées, les glaciers ont atteint des altitudes supérieures à celles que la formule permet de calculer.

Pourquoi la formule, qui donne de bons résultats dans le bas des vallées, cesse-t-elle de le faire plus en amont ?

Lorsqu'on examine la surface de glaciers de vallée actuels des Alpes ou de l'Himalaya, on constate que celle-ci peut présenter trois types de modelé :

1 - Des chutes de séracs, qui se produisent sur une rupture de pente de la vallée

2 - Des zones à forte pente, dont la surface tourmentée trahit l'existence, en profondeur, d'une vallée de forme irrégulière

3 - Enfin des zones à effet de paroi où la pente, régulière, est plus faible que dans les précédentes, tout en étant supérieure à ce que donnerait l'application de la formule.

Le tableau suivant donne, pour un certain nombre de zones de ce dernier type appartenant à des glaciers français et suisses ainsi qu'à quelques appareils himalayens, la valeur de la pente en fonction de la largeur de la vallée.

La pente est celle des zones à effet de paroi.
La largeur est mesurée au niveau de la surface du glacier.

Les résultats sont regroupés sur le graphique ci-dessous.
Les points en noir correspondent aux glaciers alpins, ceux en rouge aux glaciers himalayens.

En dépit d'une forte dispersion - due en particulier au fait que sa seule largeur ne suffit pas à caractériser une vallée - il apparaît que la pente est d'autant plus faible que la vallée est plus large.
Ce résultat n'a rien de surprenant.
En effet le mouvement d'un glacier résulte de l'action de deux forces antagonistes :

- La gravité, qui s'exerce sur la masse du glacier et qui, pour une longueur donnée du glacier ( mesurée dans le sens de sa marche ), est donc proportionnelle à la section de l'auge.
- Les forces de frottement, essentiellement contre les parois et le fond de l'auge, qui sont liées au périmètre de celle-ci.

Plus les dimensions de l'auge sont importantes, plus faible est l'influence du frottement sur le mouvement du glacier. À la limite, pour une largeur très grande, on retrouverait les résultats donnés par la formule.
Inversement, plus la vallée est étroite, plus les frottements sont importants et plus la pente du glacier doit être grande pour les vaincre.
Cet effet de paroi, classique en mécanique des fluides, est le premier de ceux que nous annoncions en tête de page et qui viennent altérer la belle simplicité de la formule.

Mais comprenons nous bien : sa largeur n'est, bien entendu, pas le seul facteur qui caractérise la forme d'une vallée et donc les pertes de charges que subit le glacier qui la parcourt. C'est seulement le paramètre le plus facile à utiliser et le seul d'ailleurs dont on dispose dans la majorité des cas.
La vallée du Rhône, entre Martigny et Léman, peut constituer un cas d'école, on le verra ici.

Le tableau ci-dessus montre que le glacier actuel le plus large (1,65 km), présentant la pente la plus faible, est celui d'Aletsch (Repère 5).
Ceci peut être mis en relation avec le fait que la vitesse maximale de ce glacier, vers la sortie de Concordiaplatz, est comparable à celle des deux glaciers groenlandais les plus rapides du monde [Les Glaciers, Amédée Zryd, éditions Pillet, 2001].
De l'ensemble des graphiques figurant sur ces pages, on peut déduire que, sous réserve des paragraphes qui vont suivre, la formule rend bien compte de l'altitude atteinte par la glace dans le bas des vallées, tant que la largeur du glacier au niveau supérieur de la glace restait supérieure aux valeurs figurant sur le graphique ci-dessus.
C'était le cas dans le bas des vallées alpines, puisque l'on relève les largeurs suivantes :

- Cluse de Voreppe : 4 km
- Grésivaudan : 6 à 8 km
- Champsaur ( au Riss ) : 4 à 8 km
- Durance : 4 à 10 km.

La meilleure démonstration de l'exactitude de la formule nous paraît être constituée par ce dernier glacier.



Il convient de garder à l'esprit que la courbe doit être considérée comme joignant entre eux les points représentatifs des sites caractéristiques les plus élevés - c'est leur enveloppe, au sens mathématique du mot - et non comme une moyenne entre tous les points figurant sur le graphique. On voit alors que, de Sisteron jusqu'au premier rétrécissement à moins de 4 km, qui se situe 108 km en amont, à Saint-Martin-de-Queyrières, tous les points se placent très correctement par rapport à la courbe.

Il en est de même pour le glacier de l'Isère ( voir à ce sujet la page Altitude atteinte par le glacier de l'Isère) où l'on remarque que les points représentatiifs des sites I1, I2, I3 et I4 se placent parfaitement sur la courbe. Les effets de paroi dans la Cluse de Voreppe, large de 4 km étaient donc négligeables.

Selon les approximations faites dans le calcul de la formule, on peut hésiter entre des valeurs de coefficient égales à 20 ou à 23.
L'application faite ci-dessus au glacier de la Durance montre que le coefficient 20 est bien celui qu'il convient d'utiliser dans la formule.

CONCLUSION CONCERNANT L'EFFET DE PAROI

De ce qui précède, nous pouvons déduire que, sous réserve des effets autres que celui de paroi (voir paragraphes suivants), la formule rend bien compte de l'altitude atteinte par la glace dans les vallées, tant que la largeur du glacier mesurée au niveau de la glace restait supérieure à une valeur que l'on peut estimer à 4 km environ.
Pour des glaciers d'une telle largeur, la pente superficielle est uniquement fonction de la distance au vallum frontal.

Pour des largeurs plus faibles, la formule ne s'applique plus, l'altitude et la pente superficielle du glacier étant alors fonction des caractéristiques de l'auge, en particulier de la largeur de celle-ci.


L'EFFET DE LOBE OU EFFET D'ETALEMENT

Le second cas où la formule ne rend pas exactement compte de la réalité se rencontre dans les lobes qui terminent, dans les plaines de piémont, les glaciers alpins ou les glaciers alaskiens.
C'est le cas de celui du Rhône, par exemple, dont le lobe terminal s'étalait en patte de lion (ou en patte d'ours ou en pecten, l'animal dépendant de l'auteur) sur le plateau molassique suisse ainsi que sur la plaine, également molassique, de La Tour du Pin.
À Martigny, par exemple, la surface du glacier ne se trouvait qu'à 1750 m [Labhart et Decrouez, 1997] - ou vers 2000 m, ainsi que semblent le montrer des études récentes - et non à 2300 m comme l'indique la formule.
Nous l'avons dit plus haut, la cause de cette divergence doit être recherchée dans le tracé des lignes de courant qui divergent dans le cas de tels lobes de piémont alors qu'elles sont parallèles dans celui d'une masse de glace de largeur infinie (ou constante), cas d'école ayant servi à l'établissement de la formule.

L'effet d'étalement est maximum dans le cas des grandes calottes glaciaires.
Les courbes ci-dessous permettent de comparer les tracés des surface de quelques calottes (Antarctique, Groenland) aux valeurs fournies par application de la formule.



On constate que celle-ci conduit toujours à des altitudes égales ou supérieures à celles de la réalité.

Dans le cas de l'Antarctique, la formule représente bien la réalité jusqu'à 300 km environ du front du glacier; plus en amont, la surface réelle se tient toujours en dessous de la valeur calculée.
Ceci n'a, a priori, rien de surprenant, puisque la formule est établie dans le cas de lignes de courant parallèles - cas d'un glacier de largeur infinie ou constante - alors que celles des glaciers de calotte divergent à partir des points culminants.

Les lobes glaciaires font l'objet d'une page spéciale Pour en savoir plus sur les glaciers du Spitzberg, d'Islande et de l'Alaska.





L'EFFET DE LANGUE

La formule conduit également à des résultats qui différent de la réalité dans la partie terminale d'une langue glaciaire, sans doute par suite de l'importance que prennent alors les termes secondaires.
Théoriquement en effet, les derniers mètres du parcours du glacier devraient se présenter sous la forme d'une surface de glace verticale ; dans la réalité, la pente des langues frontale est plus faible, ainsi que peuvent en témoigner tous ceux qui les ont parcourues, crampons aux pieds.

A remarquer que cette pente est plus soutenue pendant les phases d'avancée du glacier qu'au cours des périodes de stagnation ou de décrue.




L'EFFET DE FLOTTAISON

Pour être complet, nous mentionnerons un dernier effet, bien qu'il ne se rencontre pas dans les Alpes : lorsqu'un glacier se termine dans l'océan -- c'est le cas de ceux du Spitzberg ou d'Argentine -- les dernières longueurs du glacier sont soulevées par la poussée d'Archimède. Elles flottent et leur pente devient très faible.
Le glacier plonge alors dans l'océan par une falaise verticale de quelques dizaines de mètres de hauteur ..... et on n'oubliera pas que sa hauteur sous l'eau est encore bien plus grande.
La formule ne s'applique donc pas ici !

On voit que, lorsque le glacier se termine dans l'océan par une plate-forme flottante, la pente de surface à l'arrière de la falaise frontale est très modérée, en particulier pendant les phases de retrait.

d'après W.S.B. Paterson
The Physics of Glaciers (Pergamon Press, 1981)


Stricto sensu, cet effet ne s'est pas produit dans les Alpes au cours des glaciations quaternaires. Mais il n'est pas exclu qu'à défaut d'océan, des lacs suffisamment profonds aient pu jouer le même rôle, tels par exemple les grands lacs qui, en fin de glaciations, sont apparus dans les vallées.

Voir à ce sujet Les grands lacs quaternaires

Signalons enfin - sans aucune application aux glaciers alpins, bien entendu - que la surface d'un glacier est parfaitement horizontale lorsque celui-ci "flotte" sur un lac sous-glaciaire de grandes dimensions.
C'est le cas de la calotte antarctique dans les environs de la station de Vostok, où elle repose sur l'immense lac homonyme ( 250 x 50 km ).


QUE SE PASSAIT-IL A LA CONFLUENCE DE DEUX GLACIERS ?

On voit sur les graphiques d'altitude relatifs aux différentes vallées que les glaciers des vallées affluentes rejoignaient le glacier principal sans dénivellation de leur surface.
Le fait est particulièrement patent pour le confluent Arc - Isère, ainsi que le montre la comparaison des graphiques relatifs à ces deux rivières.

Ceci est corroboré par l'examen de la photographie suivante.

.

.

.

Un grand glacier d'Alaska, le glacier Barnard.
Ce cliché célèbre montre bien la juxtaposition des courants de glace et l'individualité des moraines.
Mais il permet de constater également que les surfaces des glaciers affluents se situent au même niveau que celle du glacier de vallée et qu'il n'existe pas de « marches d'escalier » aux confluents.

.

................... Cliché Bradford Washburn


Cette conclusion est valable sous réserve que les glaciers affluents soient des glaciers de vallée et non pas des langues glaciaires ou des glaciers de cirque qui, quant à eux, sont susceptibles de rejoindre le glacier principal par des chutes de séracs.


CONCLUSION

Les lignes qui précèdent nous permettent à présent de conclure.

La formule de Nye-Lliboutry s'applique très convenablement aux glaciers de vallées tant que la largeur de ceux-ci au niveau supérieur de la glace est suffisante, supérieure, pour donner un ordre de grandeur, à 4 km .
Elle ne peut être utilisée, par contre, ni pour une calotte glaciaire, ni dans le cas de glaciers de piémont présentant un lobe très étalé ni dans les dernières longueurs d'une langue glaciaire.

Enfin, notons que la surface d'un glacier n'obéit à la formule que si sa langue terminale est libre de fixer sa position et son altitude, ce qui est le cas d'un appareil pouvant circuler librement dans une vallée suffisamment large et descendante.
Si, par contre, il rejoint un autre glacier qui lui impose son altitude terminale ou s'il remonte une vallée "ascendante", la formule ne convient pas.
Ceci s'applique tout particulièrement aux diffluences, par exemple à celle du glacier rissien de la Durance au-dessus du Seuil Bayard.